Intermediate (strategy guide)

Adapted with permission from Glenn C. Rhoads strategy guide.

Contents 1 Loose connections 2 The useless triangle 3 Minimal edge templates 3.1 Template I 3.2 Template II 3.3 Template IIIa 3.4 Template IIIb 3.5 Template IVa 3.6 Template IVb 3.7 See also 4 Forming ladders 4.1 Ladder escapes 4.2 Ladder escape templates 4.3 The ladder escape fork 4.4 Foiling ladder escapes 4.5 Pre-ladder formations 5 Forcing moves 5.1 Breaking edge templates via forcing moves 5.2 Using forcing moves to steal territory 6 Using edge templates to block your opponent 7 On connectivity 7.1 Overlapping connections 7.2 Disjoint steps 7.3 Groups 8 Conclusion 9 See also

Loose connections

(See also the article Loose connection)

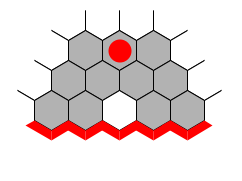
Adjacent moves provide a guaranteed connection but cover little ground. Two-bridges cover twice the distance and are almost as strong. The next best connection when even more distance is required is called the loose connection — a hex that is a two-bridge plus an adjacent step away.

The pieces of the loose connection threaten to connect via a two-bridge plus an adjacent step in two different ways — by playing at either of the marked hexes. Also, the two marked hexes are the only ones that are in the overlap of the two connection patterns. Thus, to break a loose connection, one must play in one of the marked hexes.

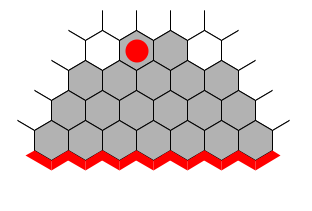
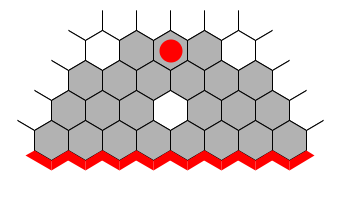
Another connection pattern that is useful to be aware of is two pieces in the same row or column that are three hexes apart.

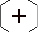The pieces threaten to connect via 2 two-bridge steps in two different ways, namely by playing at piece at one of the hexes marked with a *. There are two hexes that are in the overlap between these two connection threats and a move played in either of them breaks the immediate connection (these two hexes are marked with a +). This connection pattern is not as strong as the loose connection.

The useless triangle

(See also the article Useless triangle)

When a piece's neighboring hexes are filled by the opponent such that that piece has only two empty neighboring hexes that are also adjacent to each other, then the piece is said to lie in a "useless triangle."

		a		b		c		d		e		f		g
1
2
3
4
5
6
7

In the above diagram, the red piece at c5 and the empty hexes b6 and c6 form a useless triangle. The blue piece at e7 and the empty hexes e6 and f6 also form a useless triangle. The important point is that unless the piece in a useless triangle is in that player's border row, the piece has effectively been removed from the game — that is, it cannot have any effect on the rest of the game regardless of the rest of the position.

Minimal edge templates

An edge template is a pattern of empty hexes that will allow a piece to be connected to the edge even if the opponent has the next move. Just as the two-bridge is a useful connection pattern to know, so are minimal edge templates — the ones of the smallest size. (The templates are numbered according to row of the connecting piece).

In the templates, all points that are irrelevant for the connection are marked with a star. Important points are marked with a plus, and everything else is left empty.

Template I

Trivially, a piece on an edge row (labelled "1" in the diagram) is connected to the edge.

		a		b		c
1
2

Template II

		a		b		c		d
1
2
3

If the opponent plays inside the template, Red plays the other move in the template restoring the connection to the edge.

For templates farther away, the general strategy to apply when the opponent intrudes on the template is to make a move in the template that reduces to a smaller and closer template.

Template IIIa

(Also called Ziggurat)

		a		b		c		d		e		f
1
2
3
4

If the opponent intrudes on the template, then Red plays at one of the two marked points achieving template II. Since the c3 template and the two-chain/e3 template combination don't overlap, the opponent cannot stop both. (This template exists in a mirror image form with the red piece at e2).

Template IIIb

The clear hex in the above diagram is not part of the minimal template and can be occupied by a blue piece without disturbing the red piece's connection to the bottom edge. An intrusion can be met by two chaining either left/down or right/down to edge template II. The two two-chain/edge template II combinations do not overlap, hence blue cannot stop both threats.

Template IVa

In all cases, an intrusion can be met by reducing to a smaller edge template either by stepping one hex or by two-chaining.

Template IVb

Again, the clear hex is not part of the template and may be occupied by a blue piece without disturbing the connection to the bottom. An intrusion can be met by two chaining either left/down or right/down to edge template IIIa. The two two-chain/edge template IIIa combinations do not overlap, hence blue cannot stop both.

See also

Continue with the page Edge templates everybody should know.

Forming ladders

(See also the article Ladder)

A ladder occurs when one player tries to force a connection to an edge but is kept a constant distance away by the opponent, resulting in a sequence of moves parallel to the edge. The following is an example with Red to play.

		a		b		c		d		e		f		g		h		i
1
2
3
4
5
6
7
8
9

Suppose Red plays c8 which forces c9 in reply. Now Red can play the following forcing sequence. d8, d9, e8, e9, f8, f9, etc. A sequence of such plays parallel to an edge is called a ladder.

		a		b		c		d		e		f		g		h		i
1
2
3
4
5
6
7
8
9

Note that the Blue's responses are forced. If Red blindly continues the ladder all the way to end, then he will simply lose (Blue will get pieces in row 9 from b9 through i9). There is no good reason to ever force a ladder all the way through to end, it only helps your opponent.

Ladder escapes

(See also the article Ladder escape)

Consider the same position as before but suppose Red has an additional piece at h8.

		a		b		c		d		e		f		g		h		i
1
2
3
4
5
6
7
8
9

This additional piece forms a ladder escape which allows Red to jump a move ahead of the ladder and win the game. The piece at h2 is called the "escape piece." Red should now play along the ladder as before, forcing Blue's response at each step. After c8, c9, d8, d9, e8, e9, f8, f9, g8 Red is connected to the bottom.

		a		b		c		d		e		f		g		h		i
1
2
3
4
5
6
7
8
9

In general, for a ladder escape to be successful, it should be safely connected to the edge and not interfere with the ladder's projected path.

Ladder escape templates

(See also the article Ladder escape template)

• Row-2 ladders: All of the edge templates described earlier are valid.
• Row-3 ladders: Templates II, IIIa when the escape piece is on the near side towards the ladder, and IVa are valid.
• Row-4 ladders: Template IIIa, near side is valid. Also template IVa is valid if you can double two-bridge to the escape piece as follows.

Red can jump ahead to the escape template by playing at the marked hex.

The ladder escape fork

(See also the article Ladder escape fork)

If you are forced onto a ladder and no convenient escape is present, then you must create one. The best way is to play one of the valid ladder escape templates that threatens another strong connection. Such a move is called a ladder escape fork. For an example, see the first example in the upcoming section "forcing moves." The first forcing move is a ladder escape fork played just prior to the formation of the ladder (and a very short ladder at that). A ladder escape fork is frequently a killer move.

Foiling ladder escapes

(See also the article Foiling ladder escapes)

In order to successfully stop a ladder escape, you must either block the projected ladder path from connecting to the escape piece or intrude on the ladder escape template. To successfully stop a ladder escape fork, you need to do both with a single move and almost always with a move that is adjacent to the escape piece. The following is an example of foiling a ladder escape fork.

		a		b		c		d		e		f		g		h		i
1
2
3
4
5
6
7
8
9

Red has just played a forking ladder escape at d7. This piece is connected to the edge via template IIIa as shown by the marked hexes. Red is threatening to create an unbeatable chain by playing at E6 and the edge template is a valid ladder escape for the row-2 ladder starting G8, F9, F8, etc. To stop this, Blue needs to play a move that blocks the ladder path from connecting to the escape piece and that also intrudes on the escape template. Blue can achieve both aims by playing at D8 (which is adjacent to the escape piece). Red responds by playing C8 re-establishing the connection to the edge (there is nothing better). Now Blue continues by playing E6 blocking the forking path obtaining a winning position.

		a		b		c		d		e		f		g		h		i
1
2
3
4
5
6
7
8
9

Consider the same initial position but with Blue's piece on e7 removed.

		a		b		c		d		e		f		g		h		i
1
2
3
4
5
6
7
8
9

This change may look inconsequential but now Blue cannot foil the forking ladder escape. Suppose the play goes d8, c8, e6 as before.

		a		b		c		d		e		f		g		h		i
1
2
3
4
5
6
7
8
9

Now Red can ladder up to E8 by the sequence G8, F9, F8, E9, E8 achieving the following position.

		a		b		c		d		e		f		g		h		i
1
2
3
4
5
6
7
8
9

Now if Blue stops the e8 piece from connecting to the bottom by playing d9, Red responds by playing e7 connecting to the bottom anyway. This example illustrates that a potential foiling move that leaves vulnerable points is unlikely to succeed against a forking ladder escape. The proper handling of ladders and ladder escapes is a complex matter and it is where many games are won or lost.

Pre-ladder formations

It's important to recognize situations in which a ladder is about to form or which could be formed. Such recognition allows you to play pieces that also serve as ladder escapes before the ladder occurs. It also allows you to play defensive moves that also block potential ladder paths prior to the existence of the ladder. By far the most common pre-ladder formation is the following "Bottleneck formation."

		a		b		c		d		e		f		g
1
2
3
4
5

Red can now form a ladder by playing e4, e5, f4, f5, etc. or by playing d4, c5, c4, b5, etc. Such formations typically occur due to blocking a player from directly connecting to an edge as in the following example.

		a		b		c		d		e		f		g
1
2
3
4
5

In order to block Red from connecting to the bottom edge, Blue plays d3 creating a bottleneck. Red responds with e3 squeezing through and then Blue blocks with d5 completing the formation in the previous diagram.

The other common pre-ladder formation occurs when the defender is blocking the connection to an edge via a classic block as in the following diagram.

		a		b		c		d		e		f		g
1
2
3
4
5

Red can form a ladder by playing d3, c4 and then laddering either to the left or right (c3, b4, b3, a4 or e3, e4, f3, f4, etc.)

Forcing moves

(See also the article Forcing move)

Forcing moves are moves that make a threat that your opponent must reply to on their next turn. Common forcing moves include playing in one of the open hexes in a two-chain (threatening to break the link), intrusion into an edge template, or threatening an immediate strong connection or win. Consider the following position with the vertical player to move.

		a		b		c		d		e		f		g		h		i
1
2
3
4
5
6
7
8
9

At first glance, the position looks bad for Red, but Red can win by making a couple of forcing moves. He plays at e8 threatening to play at e7 on his next turn which would create an unbeatable winning chain. Blue has little choice but to stop this threat by playing e7 (there is nothing better). The move e8 is a forcing move.

The forcing nature of the move allows Red to place a piece on the other side of Blue's line without giving Blue any time to do anything constructive. The e8 piece on the other side is connected to the bottom and is of critical importance.

Red continues by playing another forcing move at g7. The only move that stops this piece from immediately connecting to the bottom edge is f9. But after f9, Red completes the win by playing at f8.

		a		b		c		d		e		f		g		h		i
1
2
3
4
5
6
7
8
9

The group of red pieces near the bottom are connected to the bottom edge. These pieces are connected via two-chains to the group g3-g4-f5 which is in turn connected to the top edge via edge template IIIa.

(Note: the two forcing moves could just as easily be played in the reverse order. That is Red plays g7, Blue is forced to respond with f9, and then Red plays e8 which threatens to form an unbeatable chain in two distinct ways.)

In general terms, you have three options when responding to a forcing move in a two-chain.

1. Save the link by playing the other move in the two-chain.
2. Play elsewhere (e.g. playing another move may give another way of meeting the threat thus rendering it harmless)
3. Respond with a forcing move of your own.

Breaking edge templates via forcing moves

Forcing moves are also the only way to successfully defeat an edge template. This is done by making a template intrusion that is also a more threatening forcing move. After the opponent responds to the greater threat, you can play another move within the template and destroy the connection to the edge. For example, consider the following position with the vertical player to move.

		a		b		c		d		e		f		g		h		i
1
2
3
4
5
6
7
8
9

The piece on g3 is connected to the right edge via template IIIa indicated by the '*'s. Red's best move is to play at h2. This intrudes on the edge template, is connected to the top via edge template II, and threatens to complete an unbeatable chain by playing at g2 next turn. Blue can stop this threat only by playing at g2. Then Red Plays i3 breaking Blue's connection to the right.

		a		b		c		d		e		f		g		h		i
1
2
3
4
5
6
7
8
9

Using forcing moves to steal territory

(See also the article Stealing territory)

I'll define territory to be the number of empty hexes adjacent to your pieces. By playing a forcing move in one of the empty hexes in a two-chain, a player can steal territory at no cost.

In this position, Blue has two more hexes of territory than Red (9 vs. 7 adjacent hexes). Suppose Red makes the forcing move at the indicated hex and Blue saves the link.

Now Red has two more hexes of territory; i.e. Red has stolen 4 hexes of territory without disturbing either player's connections. Significantly, the additional territory is on the other side of Blue's connection where it may potentially be used for a future threat. The additional territory can't hurt and sometimes it makes a crucial difference.

A forcing move is harmless if it gains no territory for the opponent. You should not be worried at all about leaving harmless forcing moves available for your opponent. When you have more than one way of completing a connection with a two-bridge, e.g. when completing the loose connection described previously, you should consider which forcing move is least valuable for your opponent. Consider the following position with Red to play.

		a		b		c		d		e		f
1
2
3
4
5

Red wants to connect the d4 piece to the d2 piece. There are three distinct moves that accomplish this, d3, c4 (two-chaining to d2), and c3 (two-chaining to d4).

There is not much to be said about d3; it directly connects without altering anything else. c4 connects but gives a potentially useful forcing move to Blue. Blue can respond with c3 and suppose Red saves the connection with d3. Now Blue has gained a free hex of territory, the hex c2 is now directly adjacent to the c3/b4/b5 group when it wasn't previously. Hence, c4 is worse than d3.

Now consider the last remaining possibility c3. This leaves two forcing moves for Blue but both of them are completely harmless! If after c3, Blue plays one of the forcing moves c4 or d3, then Red can save the link and Blue will not have gained any territory at all — any empty hexes adjacent to the forcing piece were already adjacent to Blue's existing pieces. Hence, c3 is just as safe as d3 but significantly, c3 gains one hex! — b3 is now adjacent to Red's d2/b3 group when it wasn't before. Thus, c3 is better than d3 and is the best of three choices.

Using edge templates to block your opponent

If your opponent has not completed an edge template but is threatening to do so in multiple ways, then the only defensive moves that stop the immediate threatened connections are those in the overlap between all threatened template connections. Suppose you are trying to stop the vertical player from connecting to the bottom edge in the following example.

		a		b		c		d		e		f
1
2
3
4
5

The vertical player has not formed an edge template but is threatening to do so in the following four different ways.

a b c d e f 1 2 3 4 5	a b c d e f 1 2 3 4 5
Two-chain to template II at d4	Adjacent move to template IIIa at d3 and e3
a b c d e f 1 2 3 4 5	a b c d e f 1 2 3 4 5
Adjacent move to template IIIa at d3	<center>Adjacent move to template IIIb at d3

The only three hexes in the overlap among all these edge templates are marked on the following diagram. To stop the immediate connection, the horizontal player must play at one of them.

		a		b		c		d		e		f
1
2
3
4
5

On connectivity

Overlapping connections

(See also the article Overlapping connections)

One should be alert to the situations where various connections, edge templates, and potential connections overlap at some hex(es). Consider the following position with Blue to move.

		a		b		c		d		e		f		g		h		i		j		k
1
2
3
4
5
6
7
8
9
10
11

At first glance, it appears that Red has an unbreakable winning path. j2 cannot be stopped from connecting to the top, j2 is connected the group f9-g9-h9-i9 through a series of unbreakable two-chains, this group is connected to e8 via a two-chain, e8 is connected to d10 via another two-chain, and d10 cannot be stopped from connecting to the bottom.

Appearances are deceiving; it is Blue that has a forced win! The flaw in Red's formation is that the two-chain from f9 to e8 and the two-chain from e8 to d10 overlap at the hex marked by a '*' in the diagram (e9). Blue should play at e9. By playing in the overlap, Blue is threatening to break both two-chains containing this hex. Red cannot save them both.

If Red responds with f8, then Blue plays d9 breaking the two-chain and establishing an unbeatable chain. If Red saves the other link by responding with d9, then Blue breaks through with f8 again establishing an unbeatable chain.

(However, Red could possibly respond with a9, so a bit more thought is required.)

Disjoint steps

When a piece can be connected to a group of pieces in one move in two non-overlapping ways, then they can be thought of as already connected to the group. Consider the following position.

		a		b		c		d		e
1
2
3
4
5

Red's three pieces are connected to the top. How can Red extend this connection downward? By playing at c4! The piece at c4 is connected to the group of three vertical pieces in two non-overlapping ways; namely, through the hexes b4 and d3. The diagrammed connection pattern is a fairly common occurrence and the connection to the piece at c4 is just as strongly connected as the pieces in a two-chain.

Groups

(See also the article Group)

A group is a collection of pieces that, considered in isolation from the rest of the position, have an unbreakable connection with each other. As you improve, it is important to learn to think in terms of safely connected groups of pieces. To illustrate why, consider the following two hex puzzles taken from Cameron Browne's book "Hex Strategy."

		a		b		c		d		e		f		g		h		i		j		k
1
2
3
4
5
6
7
8
9
10
11

It is Blue's turn; how can he win?. The chain of pieces j2-h3-f4 is connected to the right edge and furthermore, Blue has no other way of connecting to the right edge. So to win, Blue has to extend this chain to the left edge. Looked at in isolation, there doesn't seem to be any way to do this, yet by thinking in terms of connected groups, the solution falls out easily.

Notice that the j2-h3-f4 chain threatens to connect to the i7-i6-h6-h5-g6-f6-e7 group in two non-overlapping ways, through locations h4 and f5. Hence, these two groups can be thought of as a single group of pieces already connected to the right edge (this is another example of "disjoint steps"). Now notice the key hex d6. This hex threatens to connect to Blue's big group in two distinct non-overlapping ways (through e5 and d7) hence a piece played at d6 would be part of the big group (disjoint steps again!). Furthermore, a blue piece at d6 could not be stopped from connecting to the left because the c4 piece acts as a ladder escape. Therefore, d6 wins.

		a		b		c		d		e		f		g		h		i		j		k
1
2
3
4
5
6
7
8
9
10
11

Again, it is Blue's turn and the task is to win. The c4 piece cannot be stopped from connecting to the left edge since after the block a5, Red can ladder down row B to the escape piece at b9. Hence, the group c4-d3-e4 is connected to the left edge. The group j2-j3 is connected to the right edge. Blue has a third group e6-g5. If Blue can play a single move that connects the e6-g5 group to both other groups, then this would be a winning move. Blue has a unique move which does this, namely play at g4. The g4-g5-e6 group is connected to the left group through f4 and e5. It threatens to connect to the j2-j3 group via h3 and i4. h3 is directly connected to g4 and two-chains to j2. None of the hexes involved, h3, i2, and i3, is involved in the connection threat i4 plus the two chain to g5. I.e. the threats don't overlap and hence the connection cannot be stopped. Therefore, g4 wins.

There is another way of coming up with this move. Red threatens to cut off the e6-g5 group to the left by two-chaining from g3 to f5. Red is also threatening to cut off the e6-g5 from the right by two-chaining from g3 to h4. However, these threats overlap and hence, Blue can stop them both by playing in the unique hex contained in the overlap, namely g4 again.

This illustrates that offence equals defence in hex. Playing in regions of overlapping threats in order to stop all the threats is a defensive way of thinking. Trying to establish unbreakable connections between groups of your pieces is an offensive way of thinking. In this example, both offensive and defensive thinking techniques lead you to the unique best move. A lot of times defensive thinking is easier but sometimes offensive thinking is.

Conclusion

The first two strategy guides cover what I consider to be the fundamentals of hex strategy. This information should be enough to move up into the 1800s or 1900s on PlaySite. To move up the ranks of the red guys (the topmost group) requires the following. First you need to improve your opening play. Playing any reasonable looking moves during the initial phase of the game is enough for an orange player, but to compete with the reds, you need to consistently play one of the top two or maybe three moves. Unfortunately, I don't know a good way to describe how to do this; I'm not convinced the necessary information can be verbalized. After that, you need to know the Minimax principle (described in the Advanced strategy guide).

Also you need a certain mindset, call it willpower if you like, to move towards the top ranks. You have to try to hold onto every little hex the way a miser hoards gold pieces and you have use every optimization you can no matter how minor it may seem. The most useful optimizations, tricks, and special situations that I've learned so far are included in the Advanced strategy guide. But surely there are other things out there waiting to be discovered.

See also

• Basic (strategy guide)
• Advanced (strategy guide)